This website is under construction. The content of the site is being updated continuously.
The following articles will be some caculations that I'll refer to in the articles of light ray reflection without the need to include the same caculations which might shift the attention!
Obtuse Triangle
Please refer to the attached pdf-file in order to find the figure and better real text formatting. Unfortunately I chose wrong plattform. Sorry!!
Ali Salehson
Saturday, 02 January 2021
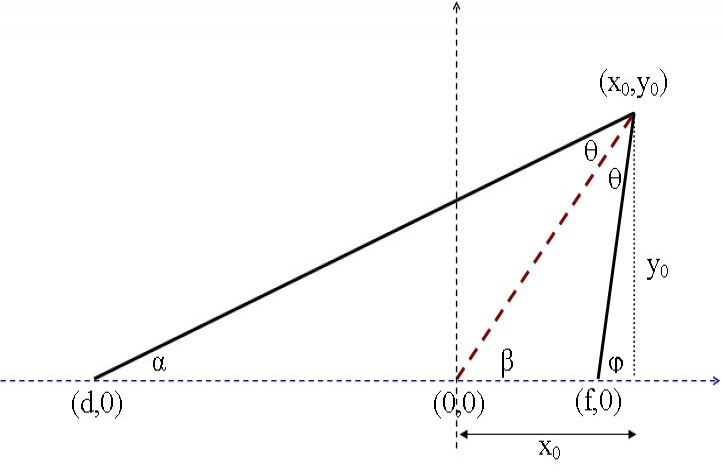
The triangle in figure is typical obtuse one i.e. the exterior angle phi is less than 90 degrees. Here the base (with altitude y0) is chosen to be on the x-axis. The bisector (the red dashed line) of the vertex angle intersects with the base at the origin point (0,0) of the Cartesian x-y coordinates. It's obvious that the tangents of the angles phi, β and α have the same numerator y0 where (x0,y0) is the vertex point.
This is because:
tan(β) = y0 / x0, tan(phi) = y0 / ( x0 -- f ) and tan(α) = y0 / (x0 -- d) , d here is negative.
The base of the triangle is consisting of two parts with lengths |f| and |d| respectively. The task is proposed to find in general the relationship between these two parts. Here is the approach!
The exterior angle phi = β + theta, while β = theta + α, which give:
2β = phi + α, and therefore tan(2β) = tan(phi + α),
By applying the tangent of the sum of angles:
(Note: in the continuation the square value will be denoted sq)
2tan(β) tan(phi) + tan(α)
--------------------- = --------------------------------
1 -- sqtan(β) 1 -- tan(phi) tan(α)
This equation can be simplified by multiplying the numerator of one side with the denominator of the other side which results another equation:
[ 2tan(β) ] [ 1 -- tan(phi) tan(α) ] = [ tan(phi) + tan(α) ] [ (1 - sqtan(β) ]
Prior continue it is important to be very careful with the +/- signs since f and d are x-coordinates. Now substitute the tangents with their values:
[ 2y0/x0 ] [ 1 -- sqy0 /( x0 -- f )(x0 -- d) ] = [ y0/( x0 -- f ) + y0 / (x0 -- d) ] [ 1 -- (sqy0/sqx0) ]
We can rewrite the above equation in order to recognize common values:
2y0 sqy0 y0 y0 sqy0
--------- [ 1 -- --------------------------- ] = [ --------------- + --------------- ] [ 1 -- ------------- ]
x0 ( x0 -- f ) (x0 -- d) ( x0 -- f ) (x0 -- d) sqx0
You may notice that y0 is common numerator on both sides of the equation which can be eliminated by dividing by y0 and we get:
2 sqy0 1 1 sqy0
-------- [ 1 -- ---------------------------- ] = [ -------------- + -------------- ] [ 1 -- ----------- ]
x0 ( x0 -- f ) (x0 -- d) ( x0 -- f ) (x0 -- d) sqx0
Further simplifying:
2 ( x0 -- f ) (x0 -- d) -- sqy0 (x0 -- d) + ( x0 -- f ) sqx0 -- sqy0
-------- [ -------------------------------------- ] = [ ------------------------------- ] [ ---------------------- ]
x0 [ (x0 -- f ) (x0 -- d) ] [ ( x0 -- f )(x0 -- d) ] sqx0
Multiplying both sides by {x0 [ ( x0 -- f ) (x0 -- d)] } will result:
sqx0 -- sqy0
2 [ (sqx0 -- sqy0) -- (f + d)x0 + f d ] = [ 2x0 -- (f + d) ] [ ---------------------- ]
x0
Multiplying both sides by x0 will result:
2(sqx0 -- sqy0)x0 -- 2(f + d)sqx0 + 2f dx0 = 2(sqx0 -- sqy0)x0 -- (f + d)sqx0 + (f + d)sqy0
2f dx0 = (f + d)sqx0 + (f + d) sqy0 = (f + d) (sqx0 + sqy0)
Obviously in this scenario, (sqx0 + sqy0) = the square of the length of the bisector (the red dashed line) which I'll denote by the letter r, and the last equation will become more simpler:
2 f d x0 = (f + d) sq(r) and can be rewritten:
2 x0 / sq(r) = (f + d) / f d, and finally:
2 x0 / sq(r) = 1/f + 1/d
This means that the task is achieved perfectly!!
Important note: I used to consider the sine and cosine functions as the normalized unit-less values of the x- and y-coordinates regardless the value of the radius of any circle.
The last equation can be modified slightly to be presented by normalized values (X, F & D) instead:
2(x0/r) = 1/(f/r) + 1/(d/r)
1 1
2 X = ----- + -----
F D
Right Angled Triangle
Please refer to the attached pdf-file in order to find the figure and better real text formatting.
Ali Salehson
Tuesday, 25 January 2021
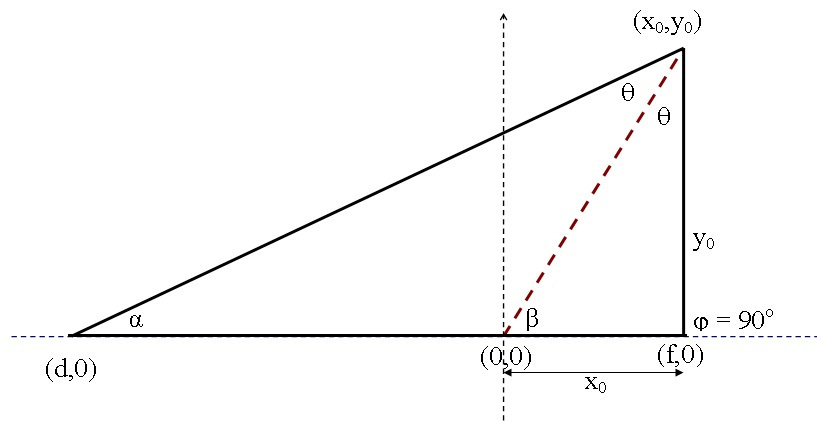
The following calculation is an extension of the obtuse triangle calculation. The triangle in figure is typical right-angled one i.e. the exterior angle phi is equal to 90 degrees.
As before the base (of the altitude y0) is chosen to be on the x-axis. The bisector (the red dashed line) of the vertex angle intersects with the base at the origin point (0,0) of the Cartesian x-y coordinates. As a result, the base of the triangle is consisting of two parts |f| and |d| and it should be obvious that f = x0 in this scenario.
The task is proposed to find the relationship between these two parts in this particular case.
Here is the approach!
It will be more convenient to avoid using the angle phi in calculations due to the fact that tan(phi) = infinity compared with the scenario presented for the obtuse triangle. Also it will be shown that the tangents of the angles theta, β and α are sufficient to find out the relationship between the two parts of the base, since it's possible to eliminate the altitude y0 from the used equations.
According to the figure of this scenario:
tan(β) = y0 / x0 , tan(theta) = x0 / y0 and tan(α) = y0 / (x0 -- d) , d here is negative!
The exterior angle β = theta + α, and this yields to:
tan(β) = tan(theta + α), and by applying the tangent of sum:
tan(theta) + tan(α)
tan(β) = ----------------------------------
1 -- tan(theta) tan(α)
The above equation can be simplified by multiplying the numerator of the left side with the denominator of the right side which results another equation:
[ tan(β) ] [ 1 -- tan(theta) tan(α) ] = [ tan(theta) + tan(α) ]
Prior continue it is important to be very careful with the +/-- signs. Now substitute the tangents by their values:
[ y0 / x0 ] [ 1 -- (x0 / y0) {y0 /(x0 -- d)} ] = [ (x0/ y0) + { y0 / (x0 -- d) } ]
We can rewrite the above equation in order to recognize common values:
y0 x0 y0 x0 y0
-------- [ 1 -- -------------------- ] = [ --------- + -------------- ]
x0 y0 (x0 -- d) y0 (x0 -- d)
You can notice that y0 can be cancelled by dividing by y0 and we get:
y0 x0 x0 y0
-------- [ 1 -- ------------ ] = [ ------- + -------------- ]
x0 (x0 - d) y0 (x0 - d)
Further simplifying:
y0 (x0 -- d) -- x0 x0 (x0 -- d) + sqy0
-------- [ ---------------------- ] = [ --------------------------------- ]
x0 (x0 - d) y0 (x0 - d)
Multiplying both sides by (x0 - d) as well as eliminating x0 will result:
y0 -- (d x0) + (sqx0 + sqy0)
-------- [ -- d ] = [ ---------------------------------------- ] and subsequently:
x0 y0
-- d sqy0 = -- d sqx0 + (sqx0 + sqy0)x0
Since (sqx0 + sqy0) = sq(r) i.e. the square of the length of the bisector (the red dashed line) which is denoted by the letter r, the last equation will become simpler by also substuting sqy0 = sq(r) -- sqx0 :
(-- d) (sq(r) -- sqx0) = -- d sqx0 + x0 sq(r)
2d sqx0 -- d sq(r) = x0 sq(r) and then: d { 2 sqx0 -- sq(r) } = x0 sq(r)
x0 sq(r)
d = ----------------------------- which can be rewritten as:
{ 2 sqx0 -- sq(r) }
x0
d = --------------------------, put it another way using the reciprocal:
2 sq(x0 /(r)) -- 1
1 1 1 1
------ = 2 (x0 /sq(r) ) -- ------ , or ------ + ------ = 2(x0 / sqr ),
d x0 d x0
then by putting x0 = f on the left side we get:
1 1
------ + ------ = 2 x0 / sq(r)
d f
However this is exactly the same relationship as with the obtuse triangle but here f = x0 when the exterior angle phi is equal to 90 degrees, i.e. the triangle is right-angled in this case.
Referring to this equation:
d {2 sqx0 -- sq(r) } = x0 sq(r) we can solve for x0: and consequently for f for this scenario:
2 d sqx0 -- d sq(r) = x0 sq(r) dividing both sides by 2d
sqx0 -- (sq(r) /2d)x0 -- sq(r) /2 = 0 which has the roots:
x0 = (sq(r)/4d) ± sqr root [ sq{ sq(r)/4d } + (sq(r)/2 ] and we choose the + value as shown in figure:
f = x0 = (sq(r)/4d) + sqr root [ sq{sq(r)/4d) + (sq(r)/2) ], I'll be discussing the -- value in future articles.
Acute Triangle
Please refer to the attached pdf-file in order to find the figure and better real text formatting.
Ali Salehson
Tuesday, 27 January 2021
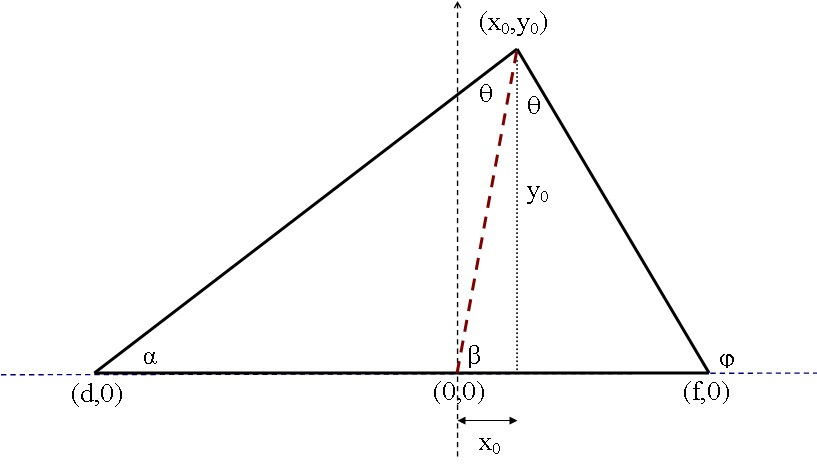
The triangle in figure is typical acute one i.e. the exterior angle phi is larger than 90 degrees.
Here the base (of the altitude y0) is chosen to be on the x-axis. The bisector of the vertex ale (the red dashed line) intersects with the base at the origin point (0,0) of the Cartesian x-y coordinates. It's obvious that the tangents of the angles phi, β and α have the same numerator y0 but this time the interior angle (180 - phi) degrees is involved, however this will result symbolically similar equations as for the obtuse triangle.
Again the base of the triangle consists of two parts |f| and |d| and the task is proposed to find in general the relationship between these two parts. Here is the approach!
The exterior angles phi = β + theta , while β = theta + α , which gives:
2β = phi + α , and therefore tan(2β) = tan(phi + α) ,
tan(β) = y0 / x0 , tan(α) = y0 / (x0 -- d) , d here is also negative!
tan(phi) = -- tan(180 -- phi) = -- y0/(f -- x0) = y0/( x0 -- f)
By applying the tangent of sum:
2tan(β) tan(phi) + tan(α)
------------------- = -----------------------------
1 -- tan2(β) 1 -- tan(phi) tan(α)
Using the same approach as for the case of the obtuse triangle will lead to the same result:
2 x0 / sq(r) = 1/f + 1/d
Geometrical Representation of Reciprocal
Please refer to the attached pdf-file in order to find the figure and better real text formatting.
Ali Salehson
Tuesday, 05 January 2021
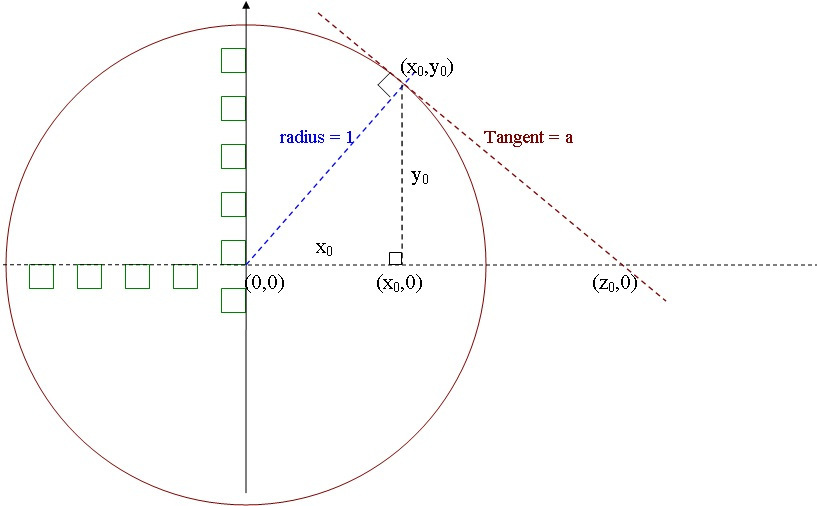
For a given value x0 of a variable x, the task is to find geometrically the reciprocal: z0 = 1 / x0
If the value 0 ≤ x0 ≤ 1 then I use the following approach. Otherwise it will be shown later that a similar approach and same figure can be applied for values larger than 1.
A unit circle, i.e. with radius r = 1 needs to be drawn with it's center at the origin (0,0) of the Cartesian x-y coordinates. It is well-known that for any circle with radius r:
sq(x)+ sq(y) = sq(r)
Then the point (x0,y0) is on the unit circle's circumference, where: y0 = sqr root of [1 -- sq(x0) ]
The tangent to the circle at the point (x0, y0) is a straight line perpendicular to the radial line from (0,0) to (x0,y0) and is intersecting the x-axis at the point (z0,0). Now it's time to prove that: z0 = 1 / x0
Let "a" denote the length of the tangent segment between points (x0, y0) and (z0,0). As shown in the figure there are three right-angled triangles. Then obviously:
sq(x0)+ sq(y0) = 1, sq(a) = sq(y0) + sq((z0 -- x0) and sq(z0) = sq(a) + 1
Solving for sq(a) = sq(y0) + sq(z0 -- x0)
sq(a) = sq(y0) + sq(z0) -- 2 z0 x0 + sq(x0)
sq(a) = 1 + sq(z0) -- 2 z0 x0 and hence: sq(z0) -- 1 = 1 + sq(z0) -- 2 z0 x0 and then:
0 = 2 -- 2 z0 x0 leading to: 2 = 2 z0 x0 or 1 = z0 x0 and finally:
z0 =1/x0
For a given value larger than 1 which can be represented by the x-coordinate of a point (z0,0) outside the circle, the reciprocal will be x0 =1/z0 using the same approach and figure.
