This website is under construction. The content of the site is being updated continuously.
Light
Welcome to this site which is providing mainly new mathematical (algebraic) analysis of the light behavior (reflection, refraction, .. etc). The content and the web pages will be published successively with time.
The website is private but not personal. The owner; me, has NOT been a member of any research group or project. The website is completely financed, managed, and edited by me and it will present extensively the results of my private hobby and interest in geometric optics of light rays. My intention is making the results available publicly as an on-line open book which may be of interest and usefulness generally or/and by professors, researchers, optics manufacturers, college and university students.
The interest and hobby in studying geometric optics has been originated from my love in basic mathematics (algebra, trigonometry, geometry, ..). Also during my studies in early years I never accepted the method to approximate the equation of reflected light rays to estimate the focal position of images formed by curvature surfaces.
I believed strongly that the reflection of light rays; for example, should be studied mathematically in proper way to find the correct equation, at least theoretically.
Studying light as RAYS wlll be the main concept throughout the site pages. Other concepts and methods (e.g. waves or photons) are outside the scope of my studies.
Ali Salehson
Friday, 01 January 2021
Gothenburg Sweden
The following articles will be some caculations that I'll refer to in the articles of light ray reflection without the need to include the same caculations which might shift the attention!
Obtuse Triangle
Please refer to the attached pdf-file in order to find the figure and better real text formatting. Unfortunately I chose wrong plattform. Sorry!!
Ali Salehson
Saturday, 02 January 2021
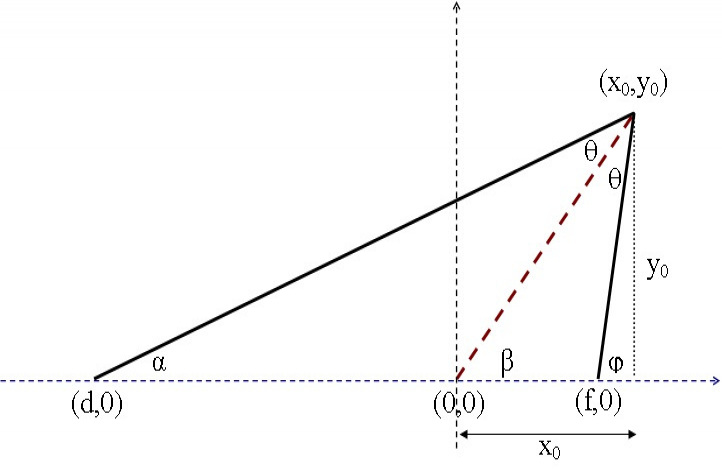
The triangle in figure is typical obtuse one i.e. the exterior angle phi is less than 90 degrees. Here the base (with altitude y0) is chosen to be on the x-axis. The bisector (the red dashed line) of the vertex angle intersects with the base at the origin point (0,0) of the Cartesian x-y coordinates. It's obvious that the tangents of the exterior angles phi, β and α have the same numerator y0 where (x0,y0) is the vertex point.
This is because:
tan(β) = y0 / x0, tan(phi) = y0 / ( x0 -- f ) and tan(α) = y0 / (x0 -- d) , d here is negative.
The base of the triangle is consisting of two parts with lengths |f| and |d| respectively. The task is proposed to find in general the relationship between these two parts. Here is the approach!
The exterior angle phi = β + theta, while β = theta + α, which give:
2β = phi + α, and therefore tan(2β) = tan(phi + α),
By applying the tangent of the sum of angles:
(Note: in the continuation the square value will be denoted sq)
2tan(β) tan(phi) + tan(α)
--------------------- = --------------------------------
1 -- sqtan(β) 1 -- tan(phi) tan(α)
This equation can be simplified by multiplying the numerator of one side with the denominator of the other side which results another equation:
[ 2tan(β) ] [ 1 -- tan(phi) tan(α) ] = [ tan(phi) + tan(α) ] [ (1 -- sqtan(β) ]
Prior continue it is important to be very careful with the +/- signs since f and d are x-coordinates. Now substitute the tangents with their values:
[ 2y0/x0 ] [ 1 -- sqy0 /( x0 -- f )(x0 -- d) ] = [ y0/( x0 -- f ) + y0 / (x0 -- d) ] [ 1 -- (sqy0/sqx0) ]
We can rewrite the above equation in order to recognize common values:
2y0 sqy0 y0 y0 sqy0
--------- [ 1 -- -------------------------- ] = [ -------------- + ------------- ] [ 1 -- ------------ ]
x0 ( x0 -- f ) (x0 -- d) ( x0 -- f ) (x0 -- d) sqx0
You may notice that y0 is common numerator on both sides of the equation which can be eliminated by dividing by y0 and we get:
2 sqy0 1 1 sqy0
-------- [ 1 -- ---------------------------- ] = [ -------------- + -------------- ] [ 1 -- ----------- ]
x0 ( x0 -- f ) (x0 -- d) ( x0 -- f ) (x0 -- d) sqx0
Further simplifying:
2 ( x0 -- f ) (x0 -- d) -- sqy0 (x0 -- d) + ( x0 -- f ) sqx0 -- sqy0
-------- [ -------------------------------------- ] = [ ------------------------------- ] [ --------------------- ]
x0 [ (x0 -- f ) (x0 -- d) ] [ ( x0 -- f )(x0 -- d) ] sqx0
Multiplying both sides by { x0 [ ( x0 -- f ) (x0 -- d)]) } will result:
sqx -- sqy0
2 [ (sqx0 -- sqy0) -- (f + d)x0 + f d ] = [ 2x0 -- (f + d) ] [ -------------------- ]
x0
Multiplying both sides by x0 will result:
2(sqx0 -- sqy0)x0 -- 2(f + d)sqx0 + 2f dx0 = 2(sqx0 -- sqy0)x0 -- (f + d)sqx0 + (f + d)sqy0
2f dx0 = (f + d)sqx0 + (f + d) sqy0 = (f + d) (sqx0 + sqy0)
Obviously in this scenario, (sqx0 + sqy0) = the square of the length of the bisector (the red dashed line) which I'll denote by the letter r, and the last equation will become more simpler:
2 f d x0 = (f + d) sq(r) and can be rewritten:
2 x0 / sq(r) = (f + d) / f d, and finally:
2 x0 / sq(r) = 1/f + 1/d
This means that the task is achieved perfectly!!
Important note: I used to consider the sine and cosine functions as the normalized unit-less values of the x- and y-coordinates regardless the value of the radius of any circle.
The last equation can be modified slightly to be presented by normalized values (X, F & D) instead:
2(x0/r) = 1/(f/r) + 1/(d/r)
1 1
2 X = ----- + -----
F D
Right Angled Triangle
Please refer to the attached pdf-file in order to find the figure and better real text formatting.
Ali Salehson
Tuesday, 25 January 2021
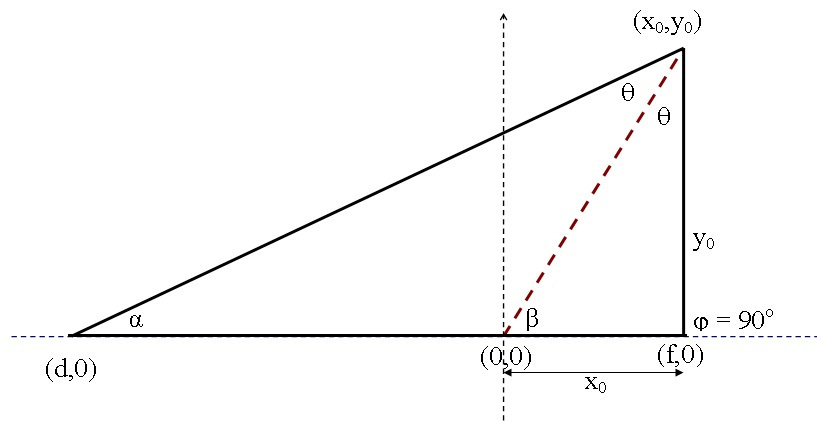
The following calculation is an extension of the obtuse triangle calculation. The triangle in figure is typical right-angled one i.e. the exterior angle phi is equal to 90 degrees.
As before the base (of the altitude y0) is chosen to be on the x-axis. The bisector (the red dashed line) of the vertex angle intersects with the base at the origin point (0,0) of the Cartesian x-y coordinates. As a result, the base of the triangle is consisting of two parts |f| and |d| and it should be obvious that f = x0 in this scenario.
The task is proposed to find the relationship between these two parts in this particular case.
Here is the approach!
It will be more convenient to avoid using the angle phi in calculations due to the fact that tan(phi) = infinity compared with the scenario presented for the obtuse triangle. Also it will be shown that the tangents of the angles theta, β and α are sufficient to find out the relationship between the two parts of the base, since it's possible to eliminate the altitude y0 from the used equations.
According to the figure of this scenario:
tan(β) = y0 / x0 , tan(theta) = x0 / y0 and tan(α) = y0 / (x0 -- d) , d here is negative!
The exterior angle β = theta + α, and this yields to:
tan(β) = tan(theta + α), and by applying the tangent of sum:
tan(theta) + tan(α)
tan(β) = ----------------------------------
1 -- tan(theta) tan(α)
The above equation can be simplified by multiplying the numerator of the left side with the denominator of the right side which results another equation:
[ tan(β) ] [ 1 -- tan(theta) tan(α) ] = [ tan(theta) + tan(α) ]
Prior continue it is important to be very careful with the +/-- signs. Now substitute the tangents by their values:
[ y0 / x0 ] [ 1 -- (x0 / y0) {y0 /(x0 -- d)} ] = [ (x0/ y0) + { y0 / (x0 -- d) } ]
We can rewrite the above equation in order to recognize common values:
y0 x0 y0 x0 y0
-------- [ 1 -- -------------------- ] = [ --------- + ------------- ]
x0 y0 (x0 - d) y0 (x0 - d)
You can notice that y0 can be cancelled by dividing by y0 and we get:
y0 x0 x0 y0
-------- [ 1 -- ------------ ] = [ ------- + ------------- ]
x0 (x0 - d) y0 (x0 - d)
Further simplifying:
y0 (x0 -- d) -- x0 x0 (x0 -- d) + sqy0
-------- [ ---------------------- ] = [ ------------------------------- ]
x0 (x0 - d) y0 (x0 - d)
Multiplying both sides by (x0 - d) as well as eliminating x0 will result:
y0 -- (d x0) + (sqx0 + sqy0)
-------- [ -- d ] = [ ---------------------------------------- ] and subsequently:
x0 y0
-- d sqy0 = -- d sqx0 + (sqx0 + sqy0)x0
Since (sqx0 + sqy0) = sq(r) i.e. the square of the length of the bisector (the red dashed line) which is denoted by the letter r, the last equation will become simpler by also substuting sqy0 = sq(r) -- sqx0 :
(-- d) (sq(r) -- sqx0) = -- d sqx0 + x0 sq(r)
2d sqx0 -- d sq(r) = x0 sq(r) and then: d { 2 sqx0 -- sq(r) } = x0 sq(r)
x0 sq(r)
d = ----------------------------- which can be rewritten as:
{ 2 sqx0 -- sq(r) }
x0
d = --------------------------, put it another way using the reciprocal:
2 sq(x0 /(r)) -- 1
1 1 1 1
------ = 2 (x0 /sq(r) ) -- ------ , or ------ + ------ = 2(x0 / sqr ) ,
d x0 d x0
then by putting x0 = f on the left side we get:
1 1
------ + ------ = 2 x0 / sq(r)
d f
However this is exactly the same relationship as with the obtuse triangle but here f = x0 when the exterior angle phi is equal to 90 degrees, i.e. the triangle is right-angled in this case.
Referring to this equation:
d {2 sqx0 -- sq(r) } = x0 sq(r) we can solve for x0: and consequently for f for this scenario:
2 d sqx0 -- d sq(r) = x0 sq(r) dividing both sides by 2d
sqx0 -- (sq(r) /2d)x0 -- sq(r) /2 = 0 which has the roots:
x0 = (sq(r)/4d) ± sqr root [ sq{ sq(r)/4d } + (sq(r)/2 ] and we choose the + value as shown in figure:
f = x0 = (sq(r)/4d) + sqr root [ sq{sq(r)/4d) + (sq(r)/2) ] , I'll be discussing the -- value in future articles.
Acute Triangle
Please refer to the attached pdf-file in order to find the figure and better real text formatting.
Ali Salehson
Tuesday, 27 January 2021
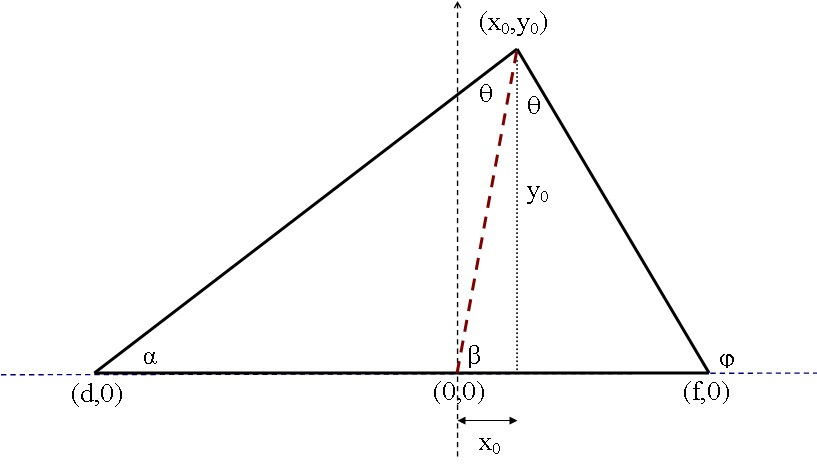
The triangle in figure is typical acute one i.e. the exterior angle phi is larger than 90 degrees.
Here the base (of the altitude y0) is chosen to be on the x-axis. The bisector of the vertex ale (the red dashed line) intersects with the base at the origin point (0,0) of the Cartesian x-y coordinates. It's obvious that the tangents of the angles phi, β and α have the same numerator y0 but this time the interior angle (180 - phi) degrees is involved, however this will result symbolically similar equations as for the obtuse triangle.
Again the base of the triangle consists of two parts |f| and |d| and the task is proposed to find in general the relationship between these two parts. Here is the approach!
The exterior angles phi = β + theta , while β = theta + α , which gives:
2β = phi + α , and therefore tan(2β) = tan(phi + α) ,
tan(β) = y0 / x0 , tan(α) = y0 / (x0 -- d) , d here is also negative!
tan(phi) = -- tan(180 -- phi) = -- y0/(f -- x0) = y0/( x0 -- f)
By applying the tangent of sum:
2tan(β) tan(phi) + tan(α)
------------------- = -----------------------------
1 -- tan2(β) 1 -- tan(phi) tan(α)
Using the same approach as for the case of the obtuse triangle will lead to the same result:
2 x0 / sq(r) = 1/f + 1/d
"salehson theorem"
of the triangle bisector
Please refer to the attached pdf-file in order to find the figure and better real text formatting.
Ali Salehson
Tuesday, 27 January 2021
For any triangle with its base (bottom side) is placed on the x-axis of the Cartesian x-y coordinates system assuming that:
- the point (0,0) is where the bisector intersects the base, and it is the reference for all measurements.
- the base will consist of two parts |f| and |d| when the reference point (0, 0) is determind by the interior bisector.
- the triangle edge vertex (facing the base) is the point (x0,y0).
- the length of the bisector; denoted by the letter r, is the length of the straight line between (0,0) and (x0,y0).
- the exterior angle phi can be 0 < phi < 180 degrees.
The following is valid: 2 x0 / sq(r) = 1/f + 1/d
All x0, f and d are variables which can be ± but for a known triangle, i.e. x0 and r are determined then the relationship between f and d is evidently expressed by the equation.
Special Cases:
1. phi = 0 means that there is no triangle: y0 = 0
2. phi = 90 means that the triangle is right-angled and f = x0
3. phi = 180 means that there is no triangle: y0 = 0
Exterior Bisector
Please refer to the attached pdf-file in order to find the figures and better real text formatting.
Ali Salehson
Saturday, 20 February 2021
Based on the “salehson theorem” of the triangle interior angle bisector, the equation:
2x0 /sq(r) = 1/f + 1/d
can be easily extended and be applied to the bisector of the exterior angle adjacent to the vertex interior angle. This article is aimed to explicate this extension.
As it has been mentioned in previous articles, the following assumptions are still valid for both the interior and exterior bisectors and should be considered strictly relative to the case presented in the accompanied figure(s).
-
Any triangle with its base (side) is placed on the x-axis of the Cartesian x-y coordinates system, the point (0,0) will be the reference point for all length (distance) measurements. This reference point is the point where the angle bisector intersects with the base.
-
The base will consist of two parts with lengths |f| and |d| due to the intersection of the interior bisector, Figures 1 & 2. These are actually distances of the vertices on the base side relative the reference point (0,0). The vertices are shown as the points (f,0) and (d,0) respectively i.e. they are obviously located on the x-axis. In the case of the exterior bisector (Figure 3) I use the more general definition of f and d as being the x-coordinates of the vertices of the base side. This definition is still valid for both types of bisector.
-
The triangle top vertex (of the interior angle facing the base) is the point (x0,y0). The coordinate y0 is the length of the altitude, i.e. the straight line through the top vertex and perpendicular (i.e. forming a right angle with) to the opposite side (the base).
-
The length of the bisector line; which is denoted by the letter r, is the length of the straight line between (0,0) and (x0,y0). This means; like for a circle: sq(r) = sq(x0) + sq(y0), This is why I do include a curve (piece of a circle circumference) in figures.
-
Since the sum of the adjacent exterior angle (2theta) and the interior vertex angle (2µ) is well known to be 180 degrees i.e. :
(2theta) + (2µ) = 180 degrees and then theta + µ = 90 degrees
This means that the two bisectors are perpendicular to each other.
Note: Please note that the top vertex interior angle is denoted by (2µ) in Figure 3. Previously this angle has been denoted by (2theta) as shown in Figures 1 and 2. On the other hand the vertex exterior angle is now denoted by (2theta) as shown in Figure 3 while previously the angle has been denoted by (2µ) as shown in Figures 1 and 2.
There is reason for this symbol exchanging which will be clearly explained in later articles.
The inherent exterior angles theta = gamma + α, and β = theta + gamma, which give:
β = 2gamma + α, or 2gamma = β -- α and therefore tan(2gamma) = tan(β – α) is the equation that is used in this article in order to derive the intended equation.
Referring to Figure 3:
tan(gamma) = y0 / x0, tan(β) = y0 / (x0 -- f), tan(α) = y0 / (d -- x0), d here is positive!
It's obvious that the tangents of these angles gamma, β and α have the same numerator y0 but this time theta half of the exterior angle is involved.
Considering the equation tan(2gamma) = tan(β – α) and by applying the tangent of angles sum:
2tan(gamma) tan(β) ̶ tan(α)
----------------------------- = ---------------------------
1 ̶ sqtan(gamma) 1 + tan(β) tan(α)
This equation can be simplified by multiplying the numerator of one side with the denominator of the other side which results another equation:
[ 2tan(gamma) ] [ 1 + tan(β) tan(α) ] = [ tan(β) ̶ tan(α) ] [ (1 ̶ sqtan(gamma) ]
Prior continue it is important to be very careful with the ± signs. Now substitute the tangents with their values:
[2y0/x0] [1 + [sqy0/{(x0 ̶ f)(d -- x0)}]] = [{y0/(x0 ̶ f)} ̶ {y0/(d ̶ x0)}] [1 ̶ {sq(y0/ x0)}]
Now by simply exchange the signs, the above equation can be rewritten:
[2y0/x0] [1 ̶ [sqy0/{(x0 ̶ f ) (x0 ̶ d)}] ] = [{y0/(x0 ̶ f)} + {y0/(x0 ̶ d)}] [1 ̶ (sqy0 / sqx0)]
The above equation is exactly the same one that has been found in the calculation of f and d when using the interior bisector. This implies that the final equation will be:
2x0/sq(r) = 1/f + 1/d
Here comes a repeated operation:
We can rewrite the last equation in order to recognize common values on both sides:
2y0 sq.y0 y0 y0 sq.y0
-------- [ 1 ̶ ------------------------- ] = [ ------------- + ------------ ] [1 -- ------------- ]
x0 ( x0 - f ) (x0 - d) ( x0 - f ) (x0 - d) sq.x0
It can be noticed that y0 is common numerator on both sides of the equation which can be eliminated by dividing by y0 and we get:
2 sq.y0 1 1 sq.y0
-------- [ 1 ̶ ------------------------- ] = [ --------------- + ------------- ] [1 ̶ ----------- ]
x0 ( x0 - f ) (x0 - d) ( x0 - f ) (x0 - d) sq.x0
Further simplifying:
2 ( x0 ̶ f ) (x0 ̶ d) ̶ sq.y0 (x0 ̶ d) + ( x0 ̶ f ) sq.x0 ̶ sq.y0
-------- [ --------------------------------------- ] = [ ------------------------------- ] [---------------------- ]
x0 [( x0 ̶ f ) (x0 ̶ d)] [( x0 ̶ f )(x0 ̶ d)] sq.x0
Multiplying both sides by x0 [( x0 ̶ f ) (x0 ̶ d)] will result:
sq.x0 ̶ sq.y0
2 [sq.x0 ̶ sq.y0 ̶ (f + d)x0 + f d ] = [ 2x0 ̶ (f + d) ] [ ---------------------- ]
x0
Again multiplying both sides by x0 the equation becomes:
2(sq.x0 ̶ sq.y0)x0 ̶ 2(f + d)sq.x0 + 2fdx0 = 2(sq.x0 ̶ sq.y0)x0 ̶ (f + d)sq.x0 +(f + d) sq.y0
On both sides the term 2(sq.x0 ̶ sq.y0) x0 can be eliminated and the equation becomes:
2 f d x0 = (f + d) sq.x0 + (f + d) sq.y0 = (f + d) (sq.x0 + sq.y0)
Since (sq.x0 + sq.y0) is equal to the square of the length of the exterior bisector (the purple dashed line) which is denoted by the letter r, and the last equation will become simpler:
2 f d x0 = (f + d) sq.r and it can be rewritten 2 x0 / sq.r = (f + d) / f d, and finally:
2 x0 / sq.r = 1/f + 1/d
Summary and Conclusions:
The following equation:
2 x0 / sq(r) = 1/f + 1/d
is valid for all cases and types of triangle angle bisection.
This equation is applicable to any single triangle with one side (called the base) is placed on the x-axis of the Cartesian xy-coordinates system such that the origin point (0,0) is determined by the intersection point between the base line (or its extension) with either the interior bisector of the top triangle vertex angle or the exterior bisector of the adjacent angle to the top triangle vertex angle.
The origin point (0,0) is called the reference point for the angle bisection.
All variables x0, f and d can be ± and they are the x-coordinates of points (x0,0), (f,0) and (d,0) respectively.
The point (x0,0) is the intersection point between the altitude of the top triangle vertex angle facing the base with the base itself. The altitude is a straight line perpendicular to the base. The length of the altitude is denoted by |y0| or just y0 when the triangle is placed upsides. With other words the altitude is the line between the vertex point (x0,y0) and the point (x0,0).
The points (f,0) and (d,0) are the vertex points of the other two triangle angles relative the chosen reference point (0,0). This means that f and d are the x-coordinates of the base endpoints. For the case of interior bisector, |f| and |d| are actually the lengths of the parts of the base.
The bisector line itself is the line between the vertex point (x0,y0) and the reference point (0,0). The length of the bisector line is denoted by r and obviously:
sq(r) = sq(x0) + sq(y0)
The two bisector lines are perpendicular to each other as it has been explained earlier in the text of this article.
For example but not only, when x0 and r are determined then the relationship between f and d is evidently expressed by the equation.
Light Reflection Equation
Ali Salehson
Saturday, 20 February 2021
Gothenburg Sweden
The law of reflection states that a reflected ray of light emerges from the reflecting surface at the same angle to the surface normal as the incident ray, but on the opposing side of the surface normal in the plane formed by the incident and reflected rays.
To make it simpler, it is supposed that the surface is man-made reflector, fine ground and very smooth surface of material. The reflector surface can be presented as a 3-D function in space and its cross section with plane can be expressed as y = f(x) in the xy-coordinates system. An example is the spherical reflector.
In the xy-plane the normal can be considered as the bisector of a triangle angle formed by the incident and reflected rays or their line extensions.
Applying the “salehson theorem” of triangle bisector will give new and simple formula for the light reflection equation.
If there is a point light source (emitting or reflecting) placed at distance d from a reference point then its image will be found at a distance f from that reference point according to the formula:
2 x0 / sq(r) = 1/f + 1/d
Where x0 and r are explained earlier in the articles of the bisector.
That’s it, This is simply the equation of the light reflection.

Geometrical Representation
of the Reciprocal
Please refer to the attached pdf-file in order to find the figure and better real text formatting.
Ali Salehson
Tuesday, 05 January 2021
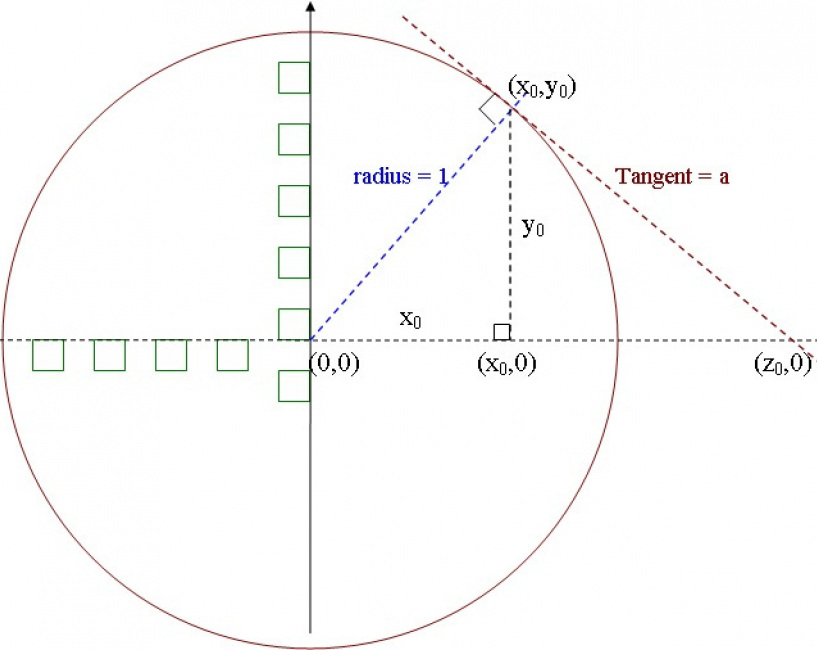
For a given value x0 of a variable x, the task is to find geometrically the reciprocal: z0 = 1 / x0
If the value 0 ≤ x0 ≤ 1 then I use the following approach. Otherwise it will be shown later that a similar approach and same figure can be applied for values larger than 1.
A unit circle, i.e. with radius r = 1 needs to be drawn with its center at the origin (0,0) of the Cartesian x-y coordinates. Then the point (x0,y0) is on the unit circle's circumference, where:
y0 = sqr root of [ 1 -- sq(x0) ] as it is known that for any circle with radius r: sq(x0) + sq(y0) = sq(r)
The tangent to the circle at the point (x0,y0) is a straight line perpendicular to the radial line from (0,0) to (x0,y0) and is intersecting the x-axis at the point (z0,0). Now it's time to prove that: z0 = 1 / x0
Let "a" denotes the length of the tangent segment between points (x0,y0) and (z0,0). As shown in the figure there are three right-angled triangles. Then obviously:
sq(x0) + sq(y0) = 1, sq(a) = sq(y0) + sq((z0 -- x0) and sq(z0) = sq(a) + 1
Solving for sq(a) = sq(y0) + sq(z0 -- x0)
sq(a) = sq(y0) + sq(z0) -- 2 z0 x0 + sq(x0)
sq(a) = 1 + sq(z0) -- 2 z0 x0 and hence: sq(z0) -- 1 = 1 + sq(z0) -- 2 z0 x0 and then:
0 = 2 -- 2 z0 x0 leading to: 2 = 2 z0 x0
or 1 = z0 x0 and finally:
z0 = 1/x0
For a given value larger than 1 which can be represented by the x-coordinate of a point (z0,0) outside the circle, the reciprocal will be x0 = 1/z0 using the same approach and figure.

Great Ziggurat of UR
The image's source: www.ancient-origins.net/ancient-places-asia/great-ziggurat-ur-001767
Great Ziggurat of Ur, c. 2100 BC, near Nasiriyah (my home city), Iraq. The ancient city UR was one of the important cities for the Sumerians.
"The Sumerians developed a complex system of metrology c. 4000 BC. This advanced metrology resulted in the creation of arithmetic, geometry, and algebra,....." read more on:
https://en.wikipedia.org/wiki/Sumer
https://en.wikipedia.org/wiki/Babylonian_mathematics
Clarification
The very first steps of a long journey have been taken by publishing the previous articles. The Chinese Lao-Tse (604 - 531 BC) said that:
“A journey of a thousand miles begins with one step.”
Until now I put a great emphasis on the equation:
2 x0 / sq(r) = 1/f + 1/d
First of all because it is based on new, second bisector theorem which is not known for anybody else but me and you cannot find it in mathematics literature or books. I have given this new theorem the name “salehson”; which is unique worldwide, in order to distinguish it from the well-known “bisector theorem” which is now not the only bisector theorem any more.
Secondly I adapted intentionally the application of the “salehson theorem” to the reflection of light rays from curved surfaces.
A generalized form of the new theorem as well as the proof is existing but not published yet. However the calculations presented in the previous articles are sufficient to give clear insight of the new theorem.
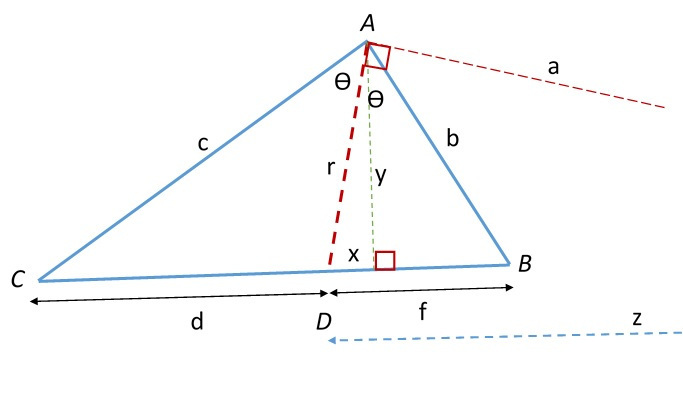
The vertex A angle: <BAC = 2·Ɵ
New salehson theorem: 2x/sq(r) = 1/f – 1/d
Well-known bisector theorem: f/d = b/c
Altitude y and foot x of the interior bisector: sq(r) = sq(x) + sq(y)
The reciprocal equation: x/r = r/z
For the triangle ABC in the above figure each small letter is the absolute value of the length of the associated line. The thick dashed red line is the interior bisector of the triangle angle <BAC. The point D is the intersection point of the bisector with the triangle side (the base) opposite to the bisected angle <BAC.
The thin dashed red line of length a is the bisector of the exterior triangle angle which meats the extension of the base CB. Z is not shown in figure but it is the intersection point of the perpendicular line to the interior bisector with the extension of the triangle side CB.
It should be understood that: x/r = r/z where z is the length of the line DZ (not shown in figure). Please refer to the article of the reciprocal.
Important:
1. There is no need any more to specify sign conventions for the equation of light ray reflection since the variables x0, d and f are x-coordinates of points on the x-axis of the x-y coordinates system. This means that the variables in the equation can be ± depending on the x value…
2. The two variables d and f are exchangeable such that the point (f,0) may be the location of the light source while the point (d,0) will be its image location.
3. Image formation of a point light source is absolutely not due to the meeting of a reflecting ray from the surface on (x0,y0) and the ray passing and reflecting along the reference x-axis. The image location f is determined by the meeting of reflected rays from the surface with the same x0 around the x-axis as it is demanded for a man-made reflector. This means that it is required to have certain symmetry or rotation property of the reflector around the x-axis such that the reflected rays forming the mage are coherent, have the same wave phase and have travelled equal optical paths.
Sunday, 04 April 2021
Ali Salehson
Gothenburg Sweden